1. 분류
분류는 연속적인 회귀와 달리 데이터 출력이 이산적인 경우를 나타냅니다.
분류:
- 이진 분류(Binary classification) : 출력의 값이 두 개인 분류
- 다중 분류(Multiclass classification) : 출력의 값이 여러개
2. 로지스틱 회귀 기법
회귀?
분류에서 사용할 수있는 로지스틱 회귀 기법에서 회귀라는 단어가 들어가 있다.
회귀와 분류에서 모두 사용이 가능합니다.
로지스틱 함수
- 로지스틱 회귀 모델 : 선형회귀의 결과를 로지스틱 함수에 적용하여 분류에 이용


선형 회귀 모델의 결과 z가 들어오면 0~1 사이의 결과값을 출력해 줍니다.
원하는threshold값을 지정하여 해당 값보다 높으면 1 낮으면 0으로 변환하여 이중 분류를 합니다.
로지스틱 회귀 모델

- 기존 선형 회귀의 경우 데이터와 특성의 조합을 통해 출력값을 예측합니다.
- 이때 출력 결과에 대해 로지스틱 함수를 거치게 되면 0과 1사이의 확률이 나온다.
- 확률값이 특정 threshold보다 높고 낮음을 판단하여 예측값을 도출한다.
이렇게 확률변환을 위해 로지스틱 함수를 사용하는 것을 로지스틱 회귀라한다.
3. 로지스틱 회귀 비용함수
최종적인 결과물은 예측값이 실제 값과 최대한 비슷하게 나오는 것이다.
최대가능도법( Maximum likelihood method)

- 상태확률이라 부른다 : 출력 y가 가질 수 있는 모든 값에 대한 확률
- y = 1 (실제 결과값) 일때 확률은 P
- P(y=1 | x,w) = p이며, p값이 1에 가까워져야 상태확률이 커진다.
- y = 0 (실제 결과값) 일때 확률은 1-P
- P(y=0 | x,w) = 1-P이며, P값이 0에 가까워져야 상태확률이 커진다.
- 즉, P값은 y값에 근접할 수록(예측을 잘할수록) 커진다.
전체 데이터 셋에 대한 상태확률

각 데이터의 상태확률을 곱한 값으로 표현이 가능하다.
따라서 전체 상태확률이 높아야 예측을 잘한 것이다.
- = 각 상태확률값이 높아야한다
- = sigmoid function을 통해 나온 값이 잘 나와야 한다.
- = 결국 선형회귀를 통한 값이 잘 나와야한다는 것이다.
- 이를 위해서는 각 데이터와 선형 곱을 하는 매개변수(특성, theta)값을 구해야한다.
매개변수 구하기
전체 상태확률 식의 경우 데이터의 갯수가 커질 수록 곱하는 데이터는 0~1사이이므로 값이 계속 줄어든다.
따라서 양변에 log를 취하고 곱하기를 더하기로 변환하여 값이 줄어드는 문제를 해결 가능하다.
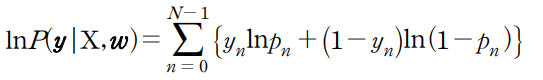
교차엔트로피오차(Cross Entropy Error)
- 최적의 매개변수를 찾는 비용함수
비용함수의 최솟값을 계산하는 알려진 해는 따로 없습니다. ( Ex. 정규방정식 ) 따라서 경사하강법이나 다른 최적화 알고리즘을 통해 찾아야한다.
경사하강법은 비용함수의 최소점을 찾아가는 알고리즘인 경우에 반해 위의 함수(최대가능도법)의 경우 최대점을 찾기 때문에 약간의 변형이 필요합니다. 따라서 위의 최대가능도법의 부호를 반전하여 새로운 함수로 만듭니다.
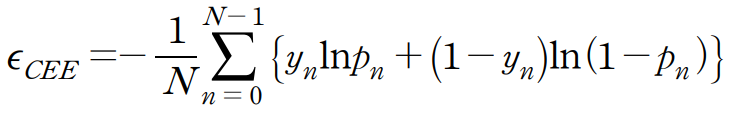
'인공지능' 카테고리의 다른 글
| [딥러닝] 딥러닝을 위한 GPU 셋팅 with VSC (0) | 2022.04.29 |
|---|---|
| DL - Text Detection (EAST) (0) | 2022.04.04 |
| 딥러닝 - VGGNet, GoogleNet (0) | 2022.03.28 |
| 딥러닝 - 합성곱 신경망 & AlexNet (0) | 2022.03.27 |
| 딥러닝 - 다중 퍼셉트론 (0) | 2022.03.21 |
![[머신러닝] - 로지스틱 회귀 (Logistic Regression)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fbj4GlS%2FbtrBuz08Fx6%2FXAr3SlDdr6vorubpw5OsyK%2Fimg.png)