머신러닝 프로세스
- 가설(Hypothesis) : 학습하고자 하는 가설을 수학적 표현식으로 나타낸다.
- 손실함수(Lost Function) : 가설의 성능을 측정할 수 있는 손실함수 정의
- 최적화 : 손실함수를 최소화 하는 학습 알고리즘 설계
선형 회귀 모델 가설

- y : 예측값, (모델 파라미터W를 사용한 가설 함수)
- n : 특성의 수
- x : 특성에 따른 값, X: 특성 벡터
- b : 편향
선형 모델의 기본 형태로 예측값(y)는 입력 특성(x)에 각 가중치(w)를 곱하여 더한 가중치의 합으로 나타낼 수 있다.
손실 함수(Cost Function)
모델의 훈련
- 모델이 훈련 세트에 가장 잘 맞도록 모델 파라미터를 설정
- 따라서 모델이 훈련 데이터에 얼마나 잘 맞는지 측정해야 한다.
- Lost Function : 성능 측정 지표
- 평균 제곱근 오차(Root mean square error)
- 평균 제곱 오차(Mean square error) : 평균 제곱근 오차보다 더 간단
MSE는 각 값과 예상값의 제곱의 평균입니다. 어떤 함수에 대해 최소값을 구하는 것은 그 함수의 제곱근을 최소화하는 것과 같습니다.


최적화 정의
정규방정식(Normal equation)

Cost function을 최소화하는 w를 구하기 위한 해석적인 방법입니다. 선형 회귀 모델을 변형하여 만들 수 있습니다.
정규방정식 - 계산 복잡도
역행렬을 구해야하므로 (n+1) * (n+1)크기를 계산해야 합니다.
따라서 일반적으로 아래와 같습니다.

또 다른 방식인 SVD(singular value decomposition, 특이값 분해)는 조금 더 짧게 걸리지만 특성의 개수가 2배로 증가하면 시간은 4배가 됩니다.

다만, 샘플의 수에 대해서는 선형적으로 증가합니다. 메모리 공간이 넉넉할 때 자주 사용할 때 효율적입니다.
경사 하강법 - Gradient Descent
Cost function을 최소화하기 위해 반복하여 파라미터를 조정해간다.

위 그림과 같이 임의의 θ에서 시작하여 한 번에 learning rate를 통해 step의 크기를 정하여 기울기가 0일 때까지 반복합니다.
따라서 learning rate에 대한 각 변화 수식은 다음과 같습니다.

Learning rate에 따른 가정
1. 학습률이 너무 적을 때
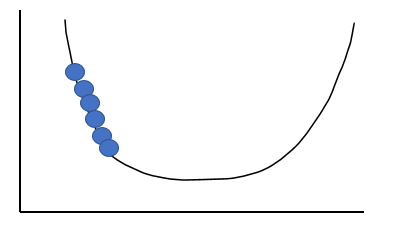
알고리즘이 수렴하기 위해 반복을 많이 해야 하므로 시간이 오래 걸린다.
2. 학습률이 너무 클 때
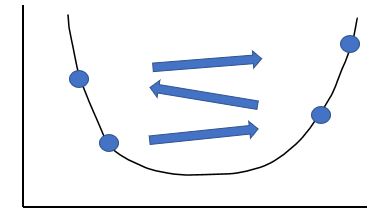
알고리즘이 수렴하는 것이 아닌 발산을 할 수도 있습니다
3. 전역 최솟값 & 지역 최솟값
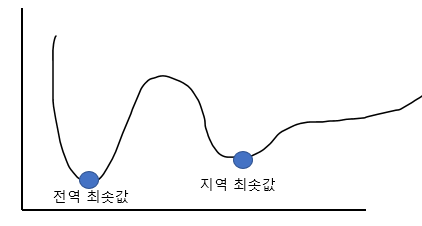
알고리즘이 왼쪽에서 부터 시작한다면 전역 최솟값에 도달할 수 있지만, 오른쪽에서 부터 시작하게 된다면 평탄한 지점을 지나기 때문에 시간도 오래 걸리고 전역 최솟값 지점이 아닌 지역 최솟값 지점에 도달할 수도 있습니다.
MSE 비용함수는 볼록 함수이므로 지역 최솟값은 없습니다.
4. 특성 스케일링과 경사 하강법

왼쪽은 특성 스케일링을 하지 않은 상태이며 오른쪽은 스케일링이 완료된 상태입니다. 두 상태 전부 최솟값에 도달하겠지만 스케일링을 하지 않은 쪽은 스케일링을 한 쪽보다 더 오랜 시간이 걸릴 것입니다.
Parameter space

일반적인 경사하강법에서 Cost function을 최소화하는 모델 파라미터를 w(or θ)는 가장 아래 있고 이 부분은 위의 전역 최솟값과 지역 최솟값이 있습니다. 따라서 모델 파라미터가 많을수록 공간의 차원은 커지고 어려워 질 것입니다.
하지만 MSE Cost function의 경우 볼록 함수로 가장 아래 지점이 지역 최솟값과 전역 최솟값이 같은 공간으로 해당 부분만 찾으면 쉽게 해결할 수 있습니다.
학습률
학습률이 너무 낮으면 많은 시간이 걸리고 너무 높으면 발산을 하게 됩니다. 따라서 너무 오래 걸리는 것을 해결하기 위해 모델의 반복 횟수를 제한합니다. 반복 횟수를 제한할 때 적당한 횟수로 해야하는데 설정하기가 쉽지 않기에 반복 횟수를 엄청 크게 잡은 후 값이 허용오차보다 작아지만 경사 하강법이 최솟값에 거의 도달했으므로 멈추게 설정합니다.
허용 오차는 작게 잡으면 잡을수록 학습 시간은 반비례하여 길어지게 됩니다.
배치 경사 하강법 - Batch gradient descent
매 경사 하강법 스텝에서 전체 훈련 세트 X에 대해 계산합니다.
즉 매 step마다 전체 훈련 데이터를 사용, 따라서 매우 느리다. 하지만 특성 수에 민감하지 않고 수십만 개의 선형 회귀를 훈련시키려면 정규 방정식이나, SVD 분해보다 더 빠르다.
확률적 경사 하강법 - Stochastic Gradient Descent
매 스텝에서 한 개의 샘플을 무작위 선택하고 하나의 샘플에 대한 gradient를 계산한다. 따라서 매우 빠른 속도이며 매 반복마다 다루는 데이터의 양이 적어 큰 훈련 세트도 훈련 가능합니다.
다만 확률적이므로 배치 경사 하강법보다 불안정하며, 최솟값에 도달하기 까지 점진적으로 도달하는 것이 아닌 요동치면서 평균적으로 도달한다. 또한 최솟값에 정확히 안착하는 것이 아닌 최솟값에 가까워지므로 구한 최솟값은 전역 최솟값이 아니다.
불안정하여 얻는 이점은 지역 최솟값을 건너뛰고 전역 최솟값에 도달할 수도 있다. 다만 위에서도 언급했듯이 구한 최솟값은 전역 최솟값이 아니다. 따라서 이를 해결하기 위해 시작했을 때에는 큰 학습률로 했다가 점진적으로 학습률을 줄이는 것이다. (= 담금질 기법, Simulated annealing) 매 반복에서 학습률을 결정하는 함수를 학습 스케쥴(Learning schedule)이라고 부른다.
SGDClassification & SGDRegressor에서는 에포크마다 모든 샘플을 사용하게 하기 위해서 훈련 세트를 섞은 후 차례대로 하나 씩 선택하고 다음 에포크에서 다시 섞는 방법 사용하며 시간이 오래걸린다.(늦게 수렴)
미니배치 경사 하강법 - Mini-Batch Gradient descent
임의의 작은 샘플 세트에 대해 gradient 계산을 진행, 미니 배치로 SGD보다 규칙적으로 최솟값에 도달하며 근접하게 도달하지만 지역 최솟값을 벗어나기는 힘듭니다. 하지만 SGD와 BGD의 장점을 모두 가져온 만큼 가장 많이 사용합니다.
| 알고리즘 | 샘플이 클때 | 외부 메모리 학습 지원 | 특성이 클때 | 스케일 조정 필요 | 사이킷런 |
| 정규방정식 | 빠름 | NO | 느림 | NO | 직접 구현 |
| SVD | 뻐룸 | NO | 느림 | NO | LinearRegression |
| 배치 GD | 느림 | NO | 빠름 | YES | SGDRegressor |
| 확률적 GD | 빠름 | YES | 빠름 | YES | SGDRegressor |
| 미니배치 GD | 빠름 | YES | 빠름 | YES | SGDRegressor |
'인공지능' 카테고리의 다른 글
| 딥러닝 - 다중 퍼셉트론 (0) | 2022.03.21 |
|---|---|
| 딥러닝 - 로지스틱 & 소프트맥스 & 크로스 엔트로피 (0) | 2022.03.15 |
| 딥러닝 - 다항 회귀 (0) | 2022.03.15 |
| 딥러닝 기초 (0) | 2022.03.13 |
| 기초 (0) | 2022.03.07 |
