다항 회귀
- 비선형 데이터를 선형 모델이 학습할 수 있게하는 기법
- 각 특성의 거듭제곱을 새로운 특성으로 추가
- Ex) PoltnomialFeatures(degree=d)는 (n+d)!/d!n! 만큼 생성
- 특정 비선형 데이터에 대해 아주 높은 고차원 다항 회귀 모델의 경우 과대적합입니다.
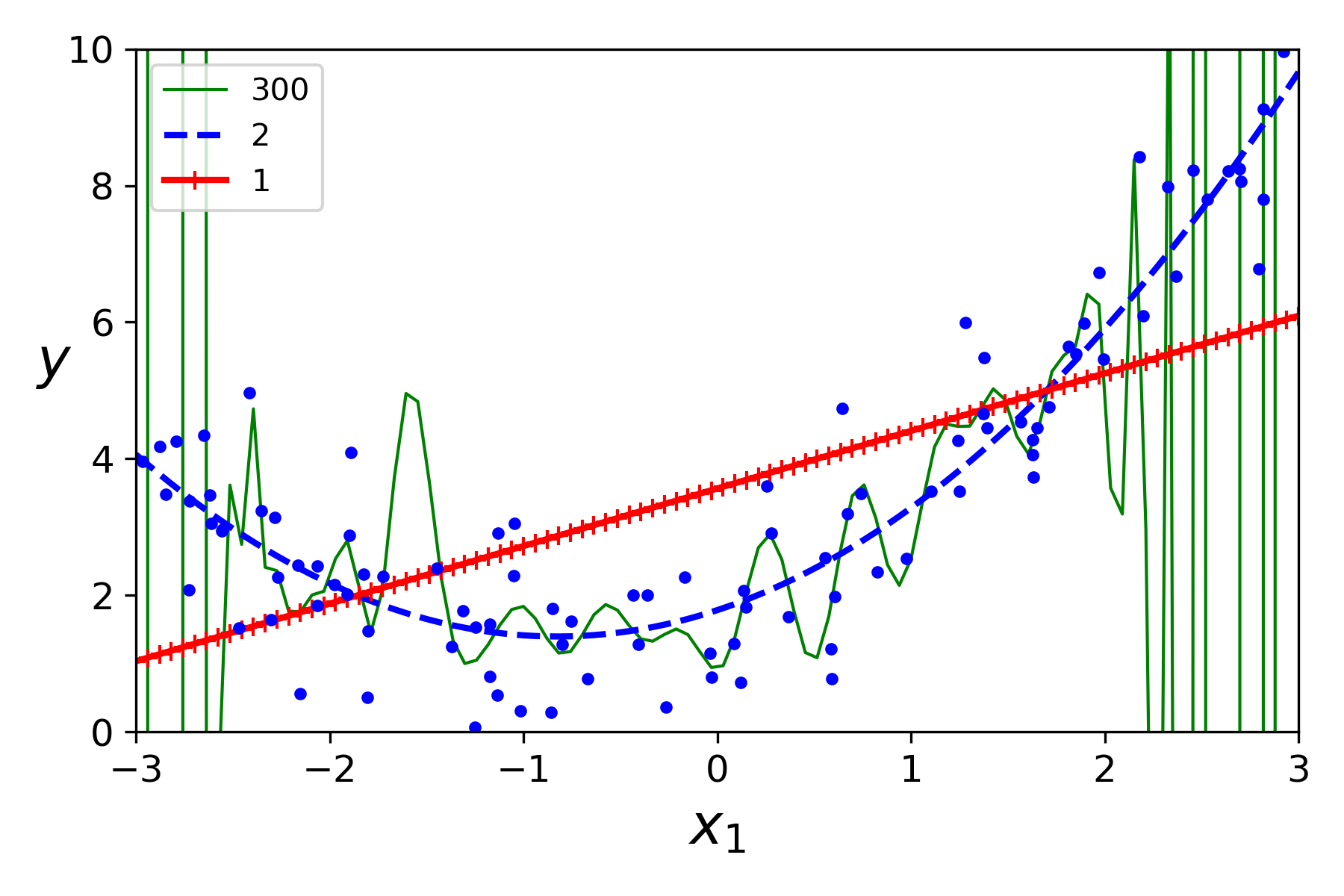
위와 같이 차원이 적을 수록 선형 모델이고 높을 수록 데이터 셋에 과대적합하는 것을 볼 수 있습니다.
과대적합 판별법
- 훈련데이터의 성능과 검증 성능 비교합니다.
- 둘다 낮으면 과소적합
- 훈련데이터는 매우 높지만 검증이 낮다면 과대적합
- 학습곡선 관찰
- 훈련세트가 추가하면서 잡음과 비선형으로 데이터와 완전히 같은 선형모델을 만들 수는 없습니다. 또한 훈련세트가 추가되어도 어느 정도까지는 오차가 상승합니다.
- 검증세트의 경우 적은 수로 훈련할 때는 제대로 일반화가 불가능하여 검증 오차가 초기에는 매우 크지만 점점 일반화하여 검증 오차가 천천히 감소합니다.
- 과대적합 모델 개선 방안
- 더 많은 훈련 데이터 추가
- 모델에 규제하여 자유도 감소


일반화 오차
- 편향 : 편향은 잘못된 가정으로 인한 것
- 편향이 큰 모델은 데이터에 과소적합되기 쉽다
- Ex) 다항 선형 모델을 일반 선형모델로 착각
- 분산 : 훈련 데이터에 있는 작은 변동에 모델이 과도하게 민감하기 때문에 나타난다.
- 자유도가 높은 모델은 높은 분산을 가지기 쉽다( 고차원 비선형 데이터의 넓게 퍼진 분포)
- 줄일 수 없는 오차 : 데이터에 존재하는 잡음
규제를 사용하는 선형 모델
- 릿지(Ridge)회귀, 라쏘 회귀, 엘라스틱넷
릿지(Ridge) 회귀터의l
- 규제가 추가된 선형 회귀
- 규제란? : 모든 특성이 출력에 주는 영향을 최소한으로 만든다( 기울기를 작게 한다.)
- 규제 : L2규제
- 방식 : 가중치(w)를 선택하며 가장 작게 유지하도록 노력한다. 또한 규제 파라미터는 훈련하는 동안에만 비용함수 내에 추가되며 훈련이 끝나면 규제가 없는 성능 지표로 평가
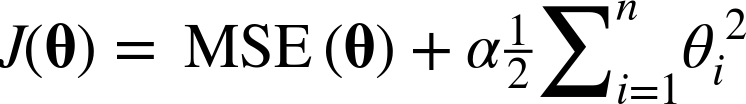
- α가 0이면 선형 회귀와 같아지며 아주 크면 모든 가중치가 거의 0에 가까워지고 데이터의 평균을 지나는 수평선이 됩니다.
라쏘(Lasso) 회귀
- 가중치 벡터의 l1노름을 사용
- 규제 : L1규제
- 특성 : 덜 중요한 특성의 가중치를 제거
- 릿지 모델과는 다르게 조금 더 작은 α값 사용
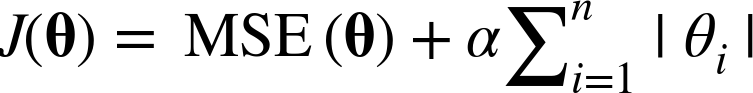
라쏘 규제 & 릿지 규제
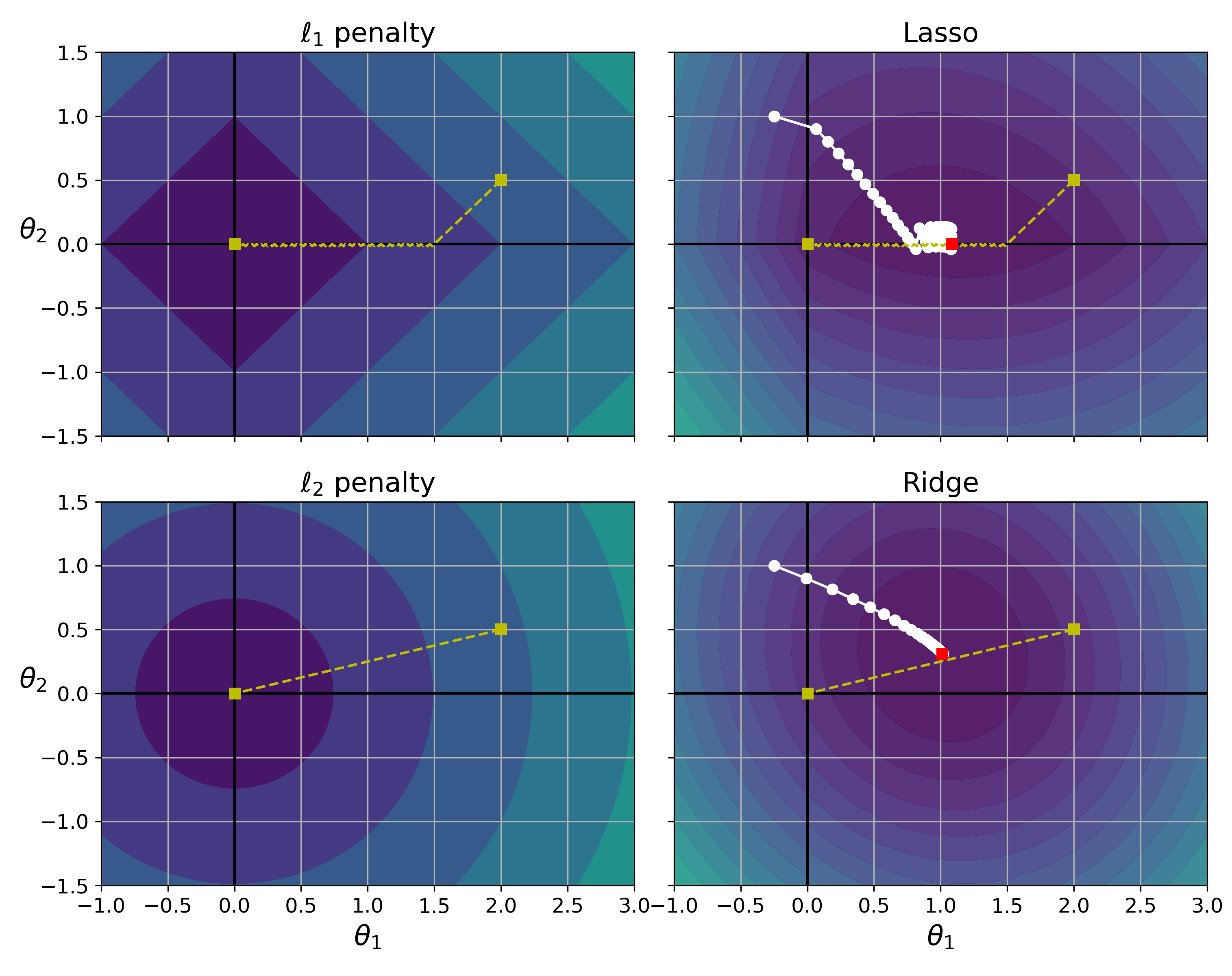
- 시작지점 : -0.25, 1 MSE 최적 파라미터 : 2, 0.5
- L1 규제 : 각 파라미터는 동일하게 감소, 최적화된 파라미터를 제외하고 나머지 파라미터 동일하게 감소시킨다.
- Lasso 손실함수 : 파라미터2가 빠르게 먼저 줄어들고 이후 파라미터1 축을 따라 전역 최저점으로 이동합니다.
- α가 증가하면 (규제 강화, 가중치가 0) 노란색 선을 따라 왼쪽으로 이동
- α가 감소하면(규제 약화, 선형 회귀와 비슷해짐) 노란색 선을 따라 오른쪽으로 이동([2, 0.5] 지점으로)
- L2 규제 : 경사하강법이 원점까지 일직선으로 따라가게 합니다.
- Ridge 손실함수 :
- 파라미터가 전역 최적점에 가까워질수록 gradient가 작아진다.(= 속도가 느려지고 진동이 없다)
- α가 증가하면 최적의 파라미터가 원점에 가까워지지만 원점이 되지는 않습니다.
엘라스틱넷 - elastic net
- 릿지 회귀와 라쏘 회귀를 절충한 모델
- 혼합 비율을 통해 두 모델의 절충안 선택
- r(rate) = 0 : 엘라스틱넷 = 릿지회귀
- r = 1 : 엘라스틱넷 = 라쏘회귀
선형 회귀 vs 릿지 vs 라쏘 vs 엘라스틱넷
- 규제가 있는 모델이 더 좋다. : 선형 회귀는 대체로 사용 안함
- 릿지가 기본, 특성이 몇개 없다면 라쏘나 엘라스틱넷 사용
- 라쏘는 기본적으로 특정 가중치를 0으로 만들어서 특성들간 관계가 강할때 사용하지 않는다.
'인공지능' 카테고리의 다른 글
| 딥러닝 - 다중 퍼셉트론 (0) | 2022.03.21 |
|---|---|
| 딥러닝 - 로지스틱 & 소프트맥스 & 크로스 엔트로피 (0) | 2022.03.15 |
| 딥러닝 - 머신러닝 기본 프로세스 (0) | 2022.03.14 |
| 딥러닝 기초 (0) | 2022.03.13 |
| 기초 (0) | 2022.03.07 |
